查核手記︰辛普森悖論

假設有100個大人及100個小孩分別到X餐廳或Y餐廳試食（只可以去其中一家），並決定是否要推薦有關餐廳，結果到X餐廳試食的100人當中，共有65人推薦，而到Y餐廳試食的100人當中則只有45人推薦。

這樣看來，X餐廳應該比較受歡迎吧？

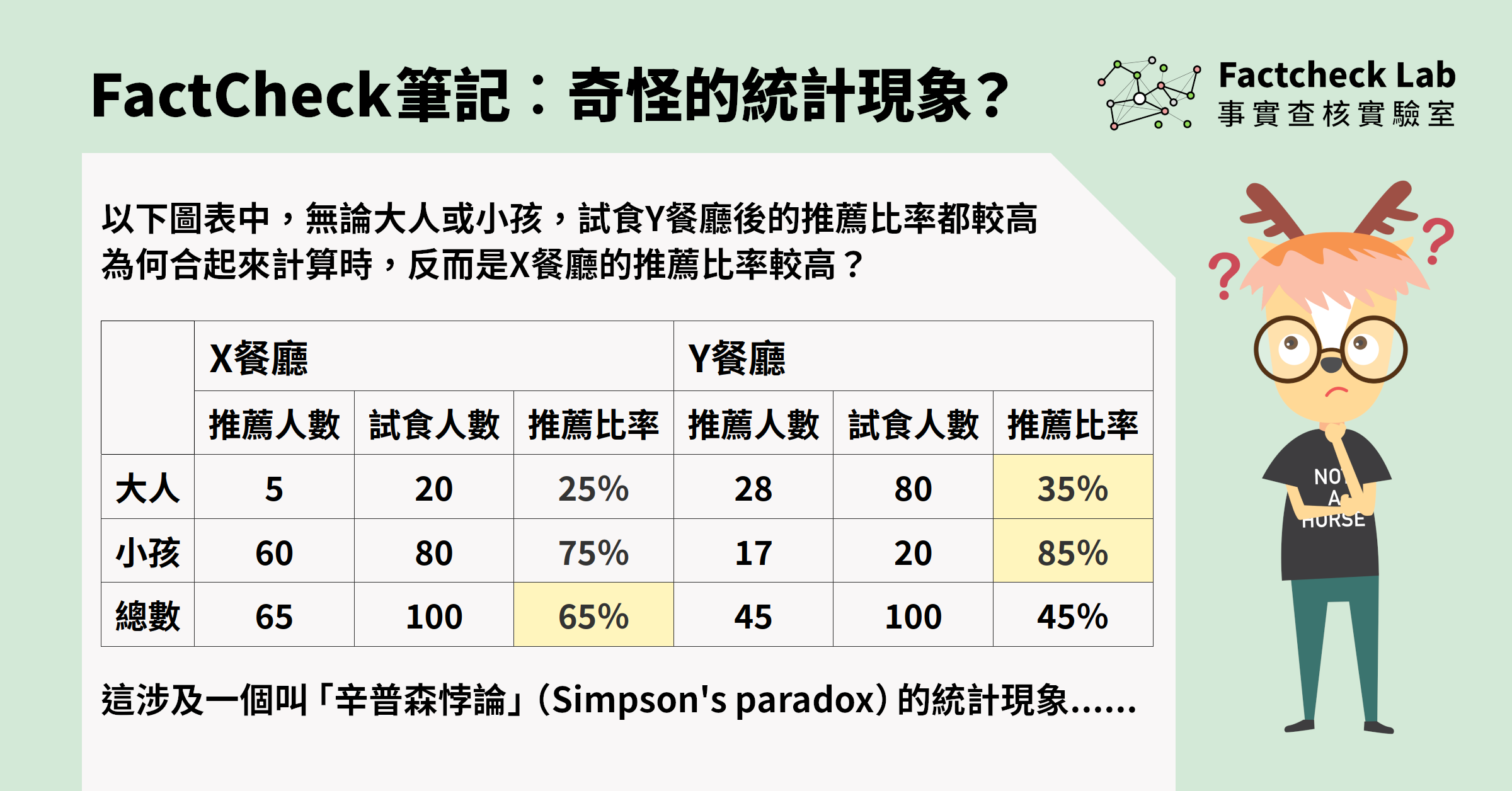
但如果大人及小孩到兩家餐廳的試食結果如下呢？

	X餐廳			Y餐廳
	推薦人數	試食人數	推薦比率	推薦人數	試食人數	推薦比率
大人	5	20	25％	28	80	35％
小孩	60	80	75％	17	20	85％
總數	65	100	65％	45	100	45％
表1

表1出現一個奇怪現象︰無論大人抑或小孩，推薦Y餐廳的比例都比X餐廳高出10%，然而一旦合起來計算，推薦比例卻反轉過來，推薦X餐廳的比例比Y餐廳高出20%。

這個現象就是統計學中的「辛普森悖論」（Simpson’s paradox）——分組的數據和整體數據呈現完全相反的趨勢。最近Factcheck Lab查核一則關於Delta變種病毒與疫苗的資訊，發現錯誤訊息源於有人演繹數據出現此現象︰

注意︰此表格展示誤導訊息的計算方法，詳見此事實查核報告分析
年齡	已接種2劑疫苗			未接種疫苗
年齡	住院人數	感染Delta病毒人數	比率	住院人數	感染Delta病毒人數	比率
<50	224	25,536	0.88%	2,290	147,612	1.55%
≥50	1,131	21,472	5.27%	670	3,440	19.48%
總數	1,355	47,008	2.88%	2,960	151,054	1.96%
表2

按年齡分組比較的話，未接種疫苗而感染Delta變種病毒人數的住院比率較高，但合起來計算卻是已接種疫苗組別較高——由於兩組別的年齡分佈不同，只看總數會得到錯誤結論。（詳情請參考Factcheck Lab的事實查核報告。）

雖然辛普森悖論看起來違反直覺，但只要仔細查看數據也不難理解。從表1我們可以注意到幾個現象︰

大人和小孩去兩家餐廳的分佈並不平均，有20%大人去了X餐廳，但有80%大人去了Y餐廳，小孩的比例則相反。
每家餐廳的試食人數分佈並不平均，X餐廳有20%大人、80%小孩試食，Y餐廳則相反。^[a]
無論是哪一家餐廳，小孩推薦的比例都明顯高於大人。

因此X餐廳的推薦比例會較受小孩的評價影響，而Y餐廳的推薦比例較受大人影響，由於小孩較傾向推薦餐廳，所以合起來計算的話，X餐廳會較具優勢。

這個悖論看來違反直覺的原因，在於呈現方式把焦點只放在推薦比率上，而忽略了產生比例的分母（即試食人數）不同，但計算整體比例時人數的差異就會影響結果。

假如去兩家餐廳試食的大人人數相同（20人），去兩家餐廳試食的小孩人數也相同（80人）（但大人和小孩的人數不必一樣），就不會產生辛普森悖論，以下例子可以說明這一點︰

	X餐廳			Y餐廳
	推薦人數	試食人數	推薦比率	推薦人數	試食人數	推薦比率
大人	5	20	25％	7	20	35％
小孩	60	80	75％	68	80	85％
總數	65	100	65％	75	100	75％
表3

另一方面，假如在同一家餐廳試食的大人與小孩人數相同，即X餐廳分別有20名大人及20名小孩試食；Y餐廳分別有80名大人及80名小孩試食，也不會產生辛普森悖論，以下例子可以說明這一點︰

	X餐廳			Y餐廳
	推薦人數	試食人數	推薦比率	推薦人數	試食人數	推薦比率
大人	5	20	25％	28	80	35％
小孩	15	20	75％	68	80	85％
總數	20	40	50%	96	160	60%
表4

如果數據涉及重要內容——例如是疫情數據——當發現各組比例有顯著分別時，我們也應該進一步了解背後是否有甚麼原因，以及如何影響結果。

除了英國的Delta變種病毒與疫苗數據外，2020年初意大利及中國的COVID-19個案死亡率（case fatality rate, CFR）數據同樣出現類似現象——若按年齡分組意大利的CFR較低，但以全部個案計算則是中國較低。詳情可參考以下這段由維多利亞大學（University of Victoria）數學及統計學助理教授Trefor Bazett拍攝的影片︰